Revisiting the Insurer’s Decision Tree Analysis Discussed in Last Tuesday’s Blog Post

Last Tuesday, we published a blog post discussing how a flawed decision tree analysis led an insurer defending a wrongful death action to reject reasonable settlement offers, and then get hit with a nearly $40 million verdict and a $7.2 million judgment for breaching a Texas state law duty to accept reasonable offers within policy limits. We concluded that the insurer’s decision tree analysis failed to prevent that fiasco primarily because the tree’s probabilities were never updated as new information became available before and during trial.

We would be remiss, however, if we did not revisit our evaluation of the insurer’s initial settlement range before the plaintiff had made any offers. Spurred by comments from decision tree analysis pioneer Marc Victor, we redid our decision tree analysis, and have concluded that the insurer’s initial settlement range made sense (although the failure to update it remained a fatal flaw). We would like to share that revised analysis with our readers because it illustrates the importance of incorporating all material uncertainties into any decision tree analysis to maximize its utility.

For purposes of this update, we are going to assume familiarity with last Tuesday’s blog post (link above), and will only reference those portions of the post relevant to the present discussion.

Briefly, we used the facts in the case discussed in last Tuesday’s post to explain the mechanics of decision tree analysis as follows:

In the case under discussion, we might say there is a 40% chance that a jury will find that the driver was not negligent when he stopped the truck on the road.

Moreover, even if a jury were to find the driver was negligent (60% chance), and it proceeds to the question of comparative fault, there is a 50% chance that the jury will find that Braswell was more than 50% responsible for the accident (which would bar recovery under Texas state law).

Using decision tree analysis, we can combine those probabilities as follows: as noted, a 40% chance of “not negligent” necessarily means a 60% chance of “negligent.” But even if there’s a 60% chance a jury will find the defendants were negligent, there’s still a 50% chance in that scenario of completely barring recovery based on Braswell’s comparative fault, which means we need to multiply the 60% by 50% (under the multiplication rule of statistics, which states that the probability that A (“negligence”) and B (“more than 50% responsibility”) both occur is equal to the probability that A occurs times the conditional probability that B occurs given that A occurs). That calculation yields a 30% chance of barring recovery based on comparative fault (even if the defendants are found negligent).

The 40% we generated above, plus the 30%, equals 70%, which means there’s a 70% chance of a defense verdict either because a jury finds the defendants were not negligent, or (negligence notwithstanding) finds that Braswell was more than 50% at fault.

Finally, for the sake of simplicity, let’s assume that the remaining 30% balance of what might happen at trial translates into a full recovery for the plaintiff (in fact, that recovery would likely be adjusted downward depending how the jury apportions fault, assuming that Braswell was less than 50% responsible for the accident, but more than 0% responsible).

With our percentages in hand, let’s look at damages. If the potential jury verdict (assuming liability) is in the range of $6-$8 million (both economic and non-economic damages), we would multiply that range by the 30% probability of a plaintiff verdict, which means an expected value for the case of $1.8 million to $2.4 million (i.e., 30% x $6-$8 million).

Readers should take note of the highlighted language above in which we assumed that the remaining 30% balance of the probabilities resulted in a 100% recovery for the plaintiff (albeit observing that the recovery would likely need to be adjusted downward depending on how the jury apportioned fault if the plaintiff was less than 50% responsible, but more than 0% responsible). That simplifying assumption resulted in an expected value for the case of $1.8 million to $2.4 million.

For pedagogical purposes — namely, explaining the mechanics of decision tree analysis — that was a reasonable assumption. But for purposes of evaluating the insurer’s initial decision tree analysis it was not. Here’s why.

After walking through the mechanics of a simplified decision tree analysis, we shared the actual decision tree analysis prepared by the insurer’s defense counsel:

Leibowitz estimated the range of a potential verdict to be between $6,000,000 and $8,000,000. He said that the plaintiffs’ expert put economic damages between $2.85 million and $3.365 million, which was “certainly reasonable.” He stated:

Based upon all the foregoing, we believe this is a defensible case on behalf of Brickman. We believe that it is likely that the jury will find that Defendants were not negligent. However, even if a jury were to find that Defendants were negligent, we believe that a jury would find a significant amount of contributory negligence on the part of Mr. Braswell with a very good chance of Plaintiff’s negligence exceeding 50%. As you know, if a jury were to determine that Plaintiff’s contributory negligence exceeded 50% he would be barred from any recovery. At this time, we believe that if we tried this case 10 times that we would get a finding of no negligence on behalf of Defendants or a verdict where Plaintiff’s negligence exceeds 50%, 7 out of 10 times. If Plaintiff’s negligence does not exceed 50%, we believe that in most cases a jury would find Plaintiff’s negligence to be in the range of 30-50%.

Leibowitz concluded that the case had a settlement value in the range of $1.25-$2 million.

Our first comment concerning that analysis questioned the initial settlement range:

Liebowitz assigned a settlement value in the range of $1.25-$2 million. However, as noted above, if Liebowitz assessed a 70% chance of a defense verdict, and total economic and non-economic damages were $6-$8 million, then the expected value of the case would be $1.8-$2.4 million (substantially higher than the range identified by Liebowitz).

The source of this discrepancy is not clear. It appears that Liebowitz might have been proposing a “low ball” settlement range below the expected value of the case. Alternatively, he may simply have made an ad hoc adjustment to the expected value based on intuition without disclosing what factors drove that modification.

After we published the article, Marc contacted us to suggest that the insurer’s initial settlement range made sense if we eliminated our simplifying assumption above that the 30% balance of the probabilities equated to a 100% recovery for the plaintiff (i.e., 0% comparative fault).

In fact, defense counsel was highly confident that the jury would apportion at least some comparative fault to the plaintiff (even if not more than 50%), stating that “[i]f Plaintiff’s negligence does not exceed 50%, we believe that in most cases a jury would find Plaintiff’s negligence to be in the range of 30-50%.” We decided to redo our decision tree analysis based on that assumption.

In Tuesday’s post, we assumed a 40% chance of a finding of “no negligence,” and a 30% chance of comparative fault in excess of 50%, resulting in a 70% chance of zero recovery. That left a 30% chance that the jury might apportion less than 50% comparative fault to the plaintiff. Let’s assume three possibilities:

• 40% comparative fault to the plaintiff (resulting in a 60% recovery)
• 25% comparative fault to the plaintiff (resulting in a 75% recovery)
• 5% comparative fault to the plaintiff (resulting in a 95% recovery).

Let’s further assume that in the scenario of a jury finding that the plaintiff was less than 50% responsible, the further downstream probabilities are:

• a 70% likelihood of finding 40% comparative fault (and 60% recovery) (since defense counsel believed that “in most cases” a jury would find Plaintiff’s negligence to be in the range of 30-50%, and “most cases” suggests considerably better odds than 50/50; as an side, he was right about that — the jury ultimately attributed 32% fault to Plaintiff)
• a 20% likelihood of finding 25% comparative fault (and 75% recovery) (to account for the possibility that defense counsel may have been too optimistic about the likelihood of a high comparative fault)
• a 10% likelihood of finding 5% comparative fault (and 95% recovery) (given the possibility that the trial judge might permit the introduction of evidence substantially weakening, or even debunking the theory of comparative fault).

In the upper nodes of our decision tree (see graphic in Tuesday’s post), this results in the following weighted average values:

• a 21% chance (70% x 30%) of a recovery range of $3,600,000-$4,800,000 (i.e., 60% recovery of $6-$8M) with an expected value range of $756,000-$1,008,000 (i.e., $3.6M x 21%-$4.8M x 21%);
• an 6% chance (20% x 30%) of a recovery range of $4,500,000-$6,000,000 (i.e., 75% recovery of $6-$8M) with an expected value range of $270,000-$360,000 (i.e., $4.5M x 6%-$6M x 6%); and
• a 3% chance (10% x 30%) of a recovery range of $5,700,000-$7,600,000 (i.e., 95% recovery of $6-$8M) with an expected value range of $171,000-$228,000 (i.e., $5.7M x 3%-$7.6M x 3%).

When you add up all the weighted values above, you get an expected value range of $1,197,000 (i.e., $$756,000 + $270,000 + $171,000) to $1,596,000 (i.e., $1,008,000 + $360,000 + $228,000). Since the remaining 70% of the scenarios (i.e., “no negligence” or “over 50% comparative fault”) yield a zero recovery, they do not change that range (see graphic in Tuesday’s post).

Here’s a graphic illustrating the calculations above, which incorporates the numbers from the graphic in Tuesday’s post:

If any readers see any errors in our calculations, please let us know.

The good news is that there is software to generate decision trees from calculations like these (we just thought it would be helpful to walk through the analysis). To illustrate a decision tree that software might generate in a case like this, Marc suggested plugging in the $6 million and $8 million as separate nodes as follows (the expected value is about $1.5 million):

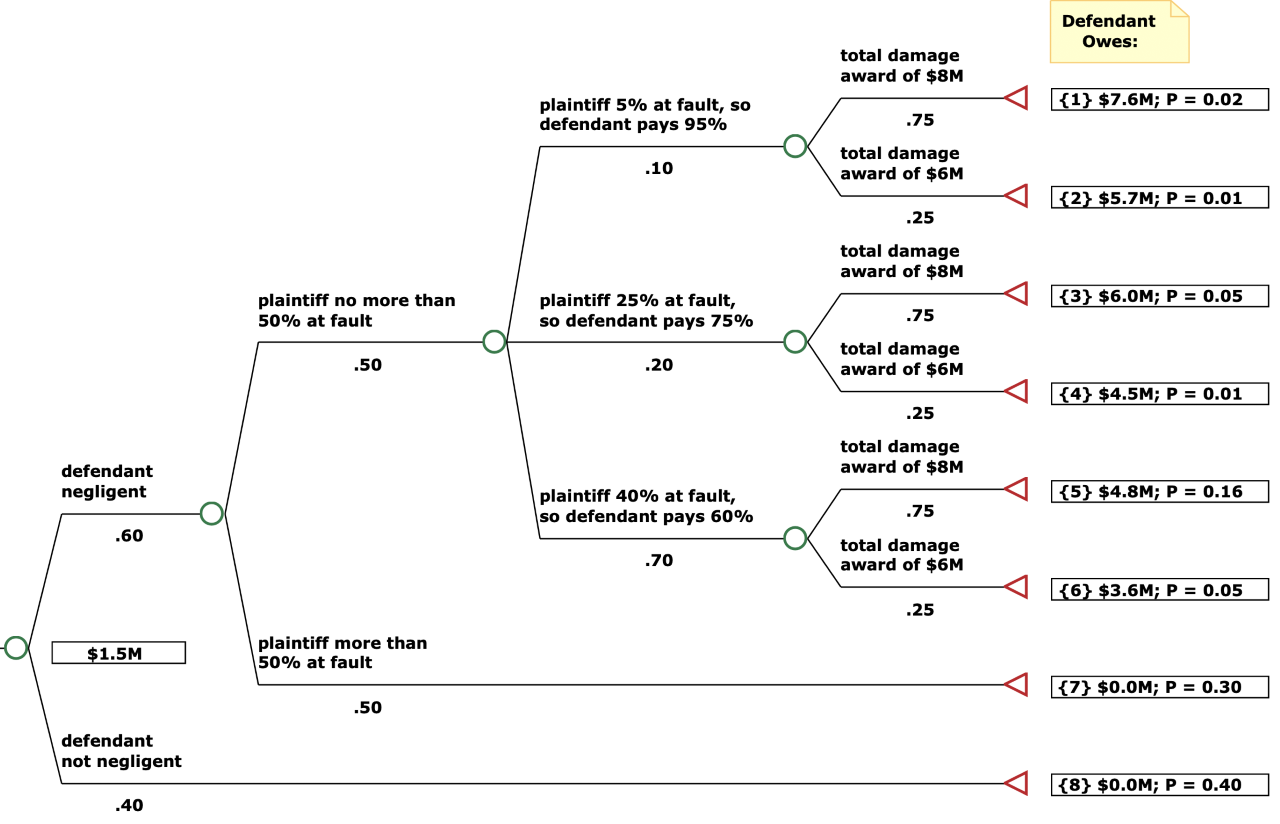
At any rate, what emerges from the analysis above is that the insurer’s initial settlement range of $1.25-$2 million was certainly reasonable, and (our bad) there is no material discrepancy from our analysis (assuming one removes the simplifying assumption we had initially made).

To be sure, the insurer had $2 million on the high end of their range, which is higher than what we calculate. But tinkering with the percentages in our spreadsheet indicates that the $2 million at the high end probably resulted from an undisclosed heavy weighting of a scenario in which the plaintiff’s comparative fault is very low (e.g., a 90% chance of 15% comparative fault). Maybe defense counsel tempered his optimism a bit in the end.

Still, as per Tuesday’s post, the problem is that the insurer did not update their analysis as the case progressed, and new information became available both from third parties and at trial. Instead, they stuck with the $2 million number for the duration of the litigation through trial as their benchmark of reasonableness for purposes of settlement negotiations.

For example, before trial, AGLIC’s representative passed along third-party assessments that the skill of plaintiff’s counsel, the pro-plaintiff leanings of the trial judge, and the impact of the sympathy factor on a jury in the relevant county, were major risks. That information surely should have caused an adjustment of the probabilities in the decision tree.

So the key takeaway from the case remains that the numbers in a decision tree are not static, and need to be updated as a case progresses and new information becomes available.