Misuse of Probability in Decision Tree Analysis: Avoiding Garbage In, Garbage Out

During our June 23 webinar on decision tree analysis, an attendee shared having heard complaints that decision tree analysis is unfair to plaintiffs because the multiple probabilities in the tree whittle down their expected damages.

However, it’s only when the “whittling down” results from misuse of the rules of probability that such criticism is warranted. A properly constructed decision tree that follows these rules will reveal risks that legitimately reduce the value of a plaintiff’s case. This blog post will explain how to correctly assign probabilities to the branches of a decision tree in a manner that avoids “garbage in, garbage out.”

Basics of Decision Tree Analysis

To recap for any readers who did not attend the webinar or are otherwise unfamiliar with the subject — decisions trees are graphical representations of the various uncertainties that comprise a lawsuit, and the probabilities of how each of those uncertainties will resolve.

For example, in a negligence case, given the evidence, the law, and the known leanings of the jury pool, what is the likelihood that the jury will find the defendant was negligent? And even if the jury finds the defendant was negligent, what is the probability that the jury will find plaintiff’s comparative fault exceeded a threshold barring recovery? And even if the jury finds that plaintiff’s comparative fault did not exceed that threshold, what percentage fault will the jury assign to the plaintiff?

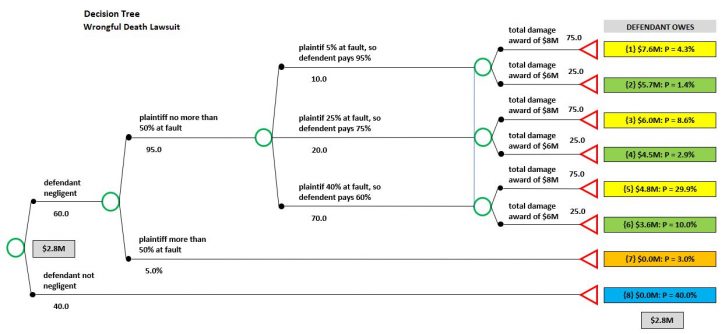
After determining the probabilities for how each of the material uncertainties in a lawsuit is likely to resolve, and entering them into a decision tree, it becomes possible to calculate the overall likelihood that each path through the tree will occur using what is known as the multiplication rule of probability (“Multiplication Rule”). That is, the probabilities along each specific path through the tree are multiplied (e.g., 60% chance that defendant will be found negligent x 75% chance that plaintiff is less than 50% at fault x 25% chance of assigning 40% fault to the plaintiff) to calculate the cumulative probability of each particular outcome.

For example, here is the decision tree for the lawsuit discussed in our recent webinar. See, for instance, the cumulative probability of the top branch — 0.60 x 0.95 x 0.10 x 0.75 = 4.3%.

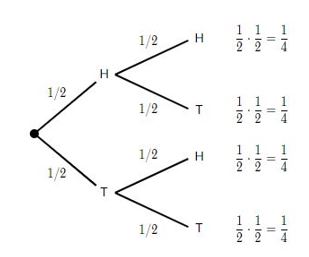
Or to use a much simpler illustration, here’s a decision tree illustrating multiplication of the probabilities of flipping a fair coin two times in a row:

The process of multiplying probabilities, however, can be abused, and such abuse has unfortunately led some to question the utility of decision tree analysis. For example, a defendant might argue that there’s a 50/50 chance they’ll prevail on their motion to dismiss, and even if they don’t, there’s a 50/50 chance they’ll prevail on their motion for summary judgment. A 50% chance of winning the case at the motion to dismiss stage, plus a 50% chance of winning the case at summary judgment (which is 50% of the remaining 50% after a loss on the motion to dismiss, or 25%), results in a 75% chance of the defendant winning even before getting to trial, and only a 25% chance that the plaintiff will even reach trial (which 25% will be further whittled down by additional uncertainties at trial). Sounds like the plaintiff is starting out behind the eight ball.

Here’s a visual of the defendant’s line of reasoning:

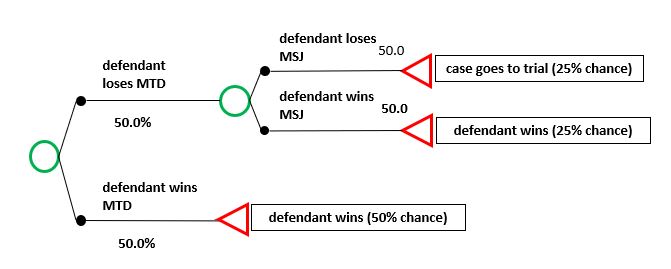
But of course, what’s good for the goose is good for the gander. The plaintiff can play this game too, arguing that there’s a 50/50 chance that defendant’s winning motion to dismiss will be reversed on appeal, and should the defendant lose its motion to dismiss, but prevail on summary judgment, there’s also a 50/50 chance that the summary judgment decision will be reversed. This turns the tables on defendant and whittles its chances of avoiding trial back down to 37.5%. Touché!

So is decision tree analysis just goofing around with numbers? Absolutely not. While the math in the above example is technically correct, both the defendant and plaintiff are misusing the Multiplication Rule. Or to put it differently, decision tree analysis is a highly effective risk management tool, but only in competent hands, and if a user puts “garbage in,” they’ll get “garbage out.” A big part of properly using decision tree analysis is understanding how the Multiplication Rule works. Let us now delve into that subject.

The Two Versions of the Multiplication Rule of Probability

Laymen who haven’t studied mathematics typically understand the multiplication rule of probability to state that the joint probability that both “A” and “B” will occur is the probability that “A” will occur times the probability that “B” will occur. Or in mathematical notation: P(A & B) = P(A) x P(B) (where “P” stands for probability).

But as Professor James Brook (formerly of New York Law School) observes in his highly recommended “A Lawyer’s Guide to Probability and Statistics,” this special form of the multiplication rule only applies if events A and B are independent.

In the parlance of probability, independence is a situation where the occurrence or non-occurrence of event A has no influence on the probability that event B will occur or not occur (and vice versa). This accurately describes the probability of two tosses of a fair coin. The probability that the second toss will land on heads is independent of the outcome of the first toss. That is, whether the first toss was heads or tails has no influence on whether the second toss will be heads or tails (i.e., for both tosses, the odds are 50/50 heads or tails).

But let’s look at a second illustration. A deck of cards contains 52 cards of which there are 13 spades, 13 hearts, 13 clubs, and 13 diamonds. What is the probability that I will pick a spade from a deck of cards? The answer is 13/52, or 25%. What’s the probability that my second selection will also be a spade?

Careful. There are two scenarios here. If I return the first selection to the deck and reshuffle, the probability of choosing a spade on the second selection remains 13/52 because there are still 52 cards and 13 spades in the deck. The two selections are independent because the card I chose for the first selection was returned to the deck and therefore has no influence on the card I choose for the second selection. I am starting from scratch.

But what if I don’t replace the first card selected. The probability of selecting a spade on the second selection then depends, or is conditional, on what card I selected on the first choice.

If I first selected a spade and removed it from the deck, then the chance of choosing a spade on the second selection is 12/51 because now there are only 12 spades in a deck of 51. But if my first selection was not a spade and I removed it from the deck, then the chance of choosing a spade on the second selection is 13/51, because while there are still 13 spades in the deck, the deck now only has 51 cards. Thus, the probability of choosing a spade on the second selection depends on, or is conditional on whether the first card removed was a spade or not. More generally, dependence exists where the outcome of the first event affects the probability of the second event.

When the outcome of one event depends on the outcome of an earlier event, the Multiplication Rule changes and the probability that both A and B will occur is the probability that A will occur times the probability that B will occur given that A has already occurred. This is what is known as a conditional probability. The mathematical notation is: P(A & B) = P(B|A) x P(A) with P(B|A) being read as the probability of B given A.

As Professor Brook explains, what the modified version of the Multiplication Rule above teaches us is that when events are dependent “attention must be paid to conditional probabilities.” This means we need to consider what the probability of the second event is given that the first event has already occurred (which will be different than the probability of the second event if the first event never occurred).

Misuse of the Multiplication Rule in Litigation

The failure to properly apply the Multiplication Rule in situations involving conditional probabilities has led to some interesting decisions shooting down attempts by one party to string together a series of unlikely events to demonstrate the improbability of its adversary’s narrative. For example, in Yassin by Yassin v. Certified Grocers of Illinois, Inc., 502 N.E.2d 315 (1986), a lawsuit was commenced on behalf of a three-year-old child who was severely injured when she placed her left hand in an operating commercial meat tenderizer. Among other defendants, the plaintiff sued the grocery store where the accident occurred (which happened to be owned by her father and uncle); the manufacturer of the meat tenderizer; and the laboratory that tested a model of the meat tenderizer.

The case went to trial, and the jury found that the meat tenderizer was not unreasonably dangerous, and therefore found the manufacturer and laboratory were not liable. However, the jury found the grocer was negligent and awarded $300,000 in damages. Plaintiff appealed the verdict in favor of the manufacturer and the laboratory on the ground that she was denied a fair trial.

One of the issues on appeal was whether the trial court had erred in allowing the testimony of an engineering professor that the probability of plaintiff’s accident was one in a billion. Specifically, the professor assigned probabilities to the following sequence of events:

(1) that an infant would wander away from its mother

(2) that the doors to the rear area of a store would be left open

(3) that boxes would be available for children to climb

(4) that a child would climb onto the boxes

(5) that a broken switch on a meat tenderizer would not be repaired

(6) that a meat tenderizer would be left running and unattended.

Multiplying the probabilities of each of these events, he concluded that the likelihood of this “bizarre string of circumstances” converging was on the order of one in a billion, and certainly not predictable by the engineers who designed the meat tenderizer.

The appellate court found this expert testimony objectionable on two grounds. First, the expert did not supply any evidentiary basis for the probabilities he assigned to each event; instead, the percentages appear to have been taken out of “thin air.” As the court explained, “no studies were presented of the number of grocery stores with doors broken, or with boxes available to be climbed; thus, [the] assignment of probabilities of these events was completely arbitrary, and an expert’s conclusions cannot be based on pure conjecture or speculation.”

Second, the court observed that the expert had misapplied the Multiplication Rule when he multiplied the probabilities he assigned to each individual event without proof of independence. As the court explained, “for this so-called ‘product rule’ to be utilized, the predicted events must be independent.”  That was clearly “not the case here, because the likelihood that a child would climb on boxes depends directly on whether those boxes were available, and it is more likely that a meat tenderizer will be left running unattended if it has a broken switch.”

In other words, the expert multiplied the probabilities of the events as if they were independent when, in fact, the probability of certain events was affected by the fact that certain other events had already occurred. For example, the expert treated the likelihood that a three-year old child would wander away from its mother as an independent event when clearly the likelihood of such a child wandering away from its mother is much higher when a box on which the child can climb is visible. Young children like climbing on boxes!

Yassin is not the first decision to have flagged abuse of the Multiplication Rule. See, e.g., People v. Collins, 438 P.2d 33, 38 (1968) (“the specific technique presented through the mathematician’s testimony and advanced by the prosecutor to measure the probabilities in question suffered from two basic and pervasive defects—an inadequate evidentiary foundation and an inadequate proof of statistical independence.”).

There are two relevant takeaways from Yassin and like decisions relevant to our discussion of decision tree analysis.

#1: Grounding Probabilities in a Decision Tree in the Evidence, the Law and Any Intangibles

The probabilities for how each uncertainty in a decision tree is likely to resolve need to be strongly grounded in the available evidence and applicable law (and any known intangible factors). To that end, during our recent webinar, we explained that this requires a group effort among attorneys knowledgeable about the case to develop and thoroughly weigh a list of reasons for why a particular uncertainty might resolve one way or the other (ideally considering the “bad” evidence and law first to mitigate confirmation bias).

For example, in the case we discussed during the webinar (Am. Guarantee & Liab. Ins. Co. v. ACE Am. Ins. Co., 413 F. Supp. 3d 583 (S.D. Tex. 2019), aff’d, 990 F.3d 842 (5th Cir. 2021)), defendants might be found negligent because there was deposition testimony from the driver that it was dangerous to park where he did, evidence that the driver stopped short, and a host of intangible factors — the plaintiffs were highly sympathetic, the plaintiffs’ attorney was highly capable, and the case was being tried before a pro-plaintiff judge and jury. On the other hand, the driver did not receive a ticket for parking where he did.

In sum, considered analysis by a team of attorneys of all of the reasons why an uncertainty may resolve in certain ways addresses the need (absent in Yassin) for an evidentiary basis for the probabilities assigned. It also illustrates why any attempt by a defendant to minimize the probability of a plaintiff’s success with a string of speculative probabilities is flawed. Instead, the defendant needs to explain the basis for its confidence in prevailing on a motion to dismiss and/or a motion for summary judgment. For example, on the former, what key allegations are missing from the complaint that render plaintiff’s claims inadequately plead? And with respect to summary judgment, on what key elements of plaintiff’s claim and/or defendant’s affirmative defenses are there likely to be no disputes of material fact? Concerning the latter, it is typically extremely difficult to reliably predict one’s chances of winning summary judgment without the benefit of discovery, and thus there’s often little evidentiary basis for estimating the probability of prevailing on a motion for summary judgment before discovery concludes.

#2: Evaluating Independence of Probabilities

When constructing a decision tree, parties and any neutrals must consider conditional probabilities. For example, in the case we discussed during the webinar (Am. Guarantee & Liab. Ins. Co., supra), a prominent Houston-area attorney had advised counsel at one of the insurance companies that a Harris County jury would never find that the deceased was more than 50% at fault (thus barring recovery) after finding that the defendant was negligent. This anecdotal evidence (which should obviously be confirmed with other experienced attorneys) indicates that the probability that a jury will find that the deceased’s comparative fault exceeds 50% depends upon whether the jury finds that the defendant was negligent.

Of course, as a matter of sequence, the jury only reaches the question of comparative fault after finding that the defendants was negligent (since absent negligence, defendants win). But we are speaking here of statistical dependence, and therefore the point is that when the jury deliberates, the probability of how a jury decides the issue of comparative fault is heavily influenced by (i.e,. not statistically independent of) the finding of negligence (whereas the issue of comparative fault might be decided very differently if considered in complete isolation from the question of negligence).

This makes sense. Once a jury finds that a defendant was negligent, it means the jury believes that the defendant somehow acted improperly, and thus will be less inclined to deny a plaintiff any recovery (albeit, in less plaintiff-friendly counties, this linkage may be less of an issue). Couple this inclination with other evidence tending to show that plaintiff was less than 50% at fault, the likelihood of defendants getting off the hook based on comparative fault is slim.

The principle of conditional probabilities thus yields a second objection to any attempt to string together speculative probabilities as part of a decision tree analysis. Specifically, a decision on a defendant’s motion for summary judgment will necessarily be rendered well after a decision on any motion to dismiss. That earlier decision will often provide insight into the judge’s thinking about the case that will influence the probability of prevailing on a motion for summary judgment. Thus, it would likely be speculative to estimate the probability for prevailing on a motion for summary judgment without first reviewing the decision on an earlier motion to dismiss.

To be sure, as part of an early case assessment, a defendant might persuasively argue that it has independent grounds to prevail on both a motion to dismiss (certain key allegations are missing from the complaint) and a motion for summary judgment (certain material facts will definitely not be in dispute). In which case, it might be acceptable to multiple the probabilities of prevailing on both. But that is only because the defendant satisfied the two requirements necessary to apply the special form of the Multiplication Rule (i.e., P(A) x P(B) rather than P(B|A) x P(A)): an adequate evidentiary foundation and adequate proof of statistical independence.

In sum, to avoid “garbage in, garbage out,” users of decision trees need to properly apply the Multiplication Rule. If you think a particular decision tree misuses that rule, challenge the probabilities.

If you missed our June 23 webinar on decision tree analysis, you can download a replay here.

We also invite readers to join our Decision Tree Analysis group on LinkedIn.